- Published on
ARTS 第30周
- Authors

- Name
- Jason Yang
- Algorithm: 961. N-Repeated Element in Size 2N Array
- Review: Thread-Safe Collections
- Tip: 10进制计数法和2进制计数法
- Share: AOP入门分享PPT
Algorithm
package org.nocoder.leetcode.solution;
import java.util.HashMap;
import java.util.Map;
/**
* 961. N-Repeated Element in Size 2N Array
*
* In a array A of size 2N, there are N+1 unique elements, and exactly one of these elements is repeated N times.
*
* Return the element repeated N times.
*
*
* Example 1:
*
* Input: [1,2,3,3]
* Output: 3
* Example 2:
*
* Input: [2,1,2,5,3,2]
* Output: 2
* Example 3:
*
* Input: [5,1,5,2,5,3,5,4]
* Output: 5
*
*
* Note:
*
* 4 <= A.length <= 10000
* 0 <= A[i] < 10000
* A.length is even
*
* @author jason
* @date 2019/2/17.
*/
public class NRepeatedElementinSize2NArray {
public static int repeatedNTimes(int[] arr) {
// 4 <= A.length <= 10000, A.length is even
if(arr == null || (arr.length < 4 || arr.length > 10000) || (arr.length % 2 != 0)){
throw new IllegalArgumentException();
}
Map<Integer, Integer> elements = new HashMap<>();
for (int i = 0; i < arr.length; i++) {
if (arr[i] < 0 || arr[i] >= 10000){
throw new IllegalArgumentException();
}
if(elements.put(arr[i],1) != null){
return arr[i];
}
}
return 0;
}
public static void main(String[] args) {
int[] arr = new int[]{5,1,5,2,5,3,5,4};
System.out.println(repeatedNTimes(arr));
}
}
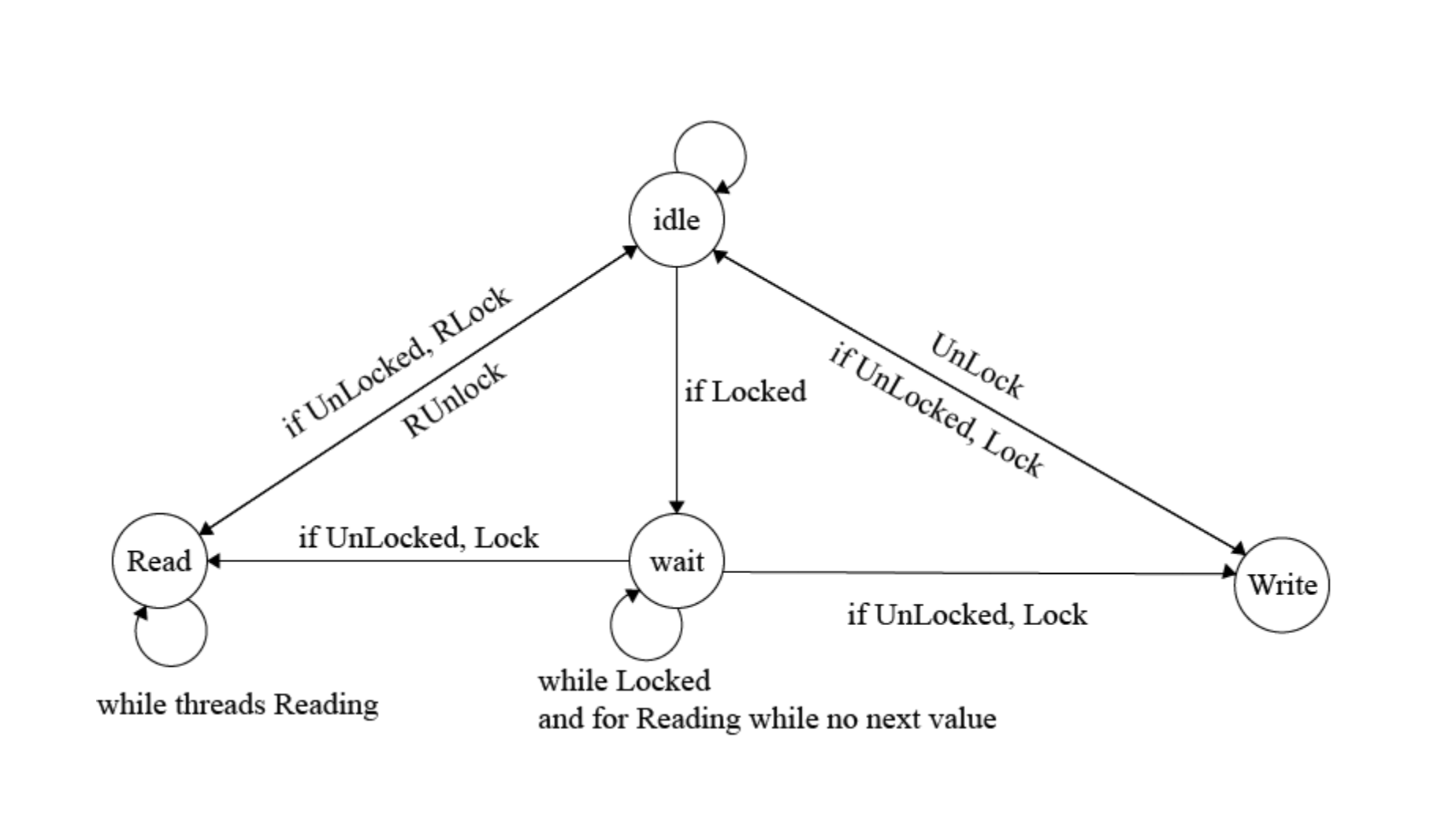
Review
Thread-Safe Collections
- 为什么需要线程安全的集合
- 多线程同时写出
- 同时读写
- 多线程同时读
- 写之前读
- 什么是线程安全的集合
- 线程安全集合是可以在没有竞争条件的情况下同时由多个线程访问的集合
- 怎么工作的
- 如何使用
- Java
java.util.concurrent包下的BlockingQueue,ConcurrentHashMap,ConcurrentSkipListMap - Python
Queue,Deques - Go 中
channels
- Java
Tip
10进制计数法和2进制计数法
最近买了一本《程序员的数学》,放假前一天拿到手,赶紧拆开读了几页,看到讲10进制和2进制的时候,茅塞顿开,感觉非常爽,以前总感觉没有把这两个计数法搞清楚(没有认真学习过,惭愧),看完之后迫不及待的找了一些数字算了起来。如果有跟我一样的兄弟们,建议快快拿起这本书读起来吧。
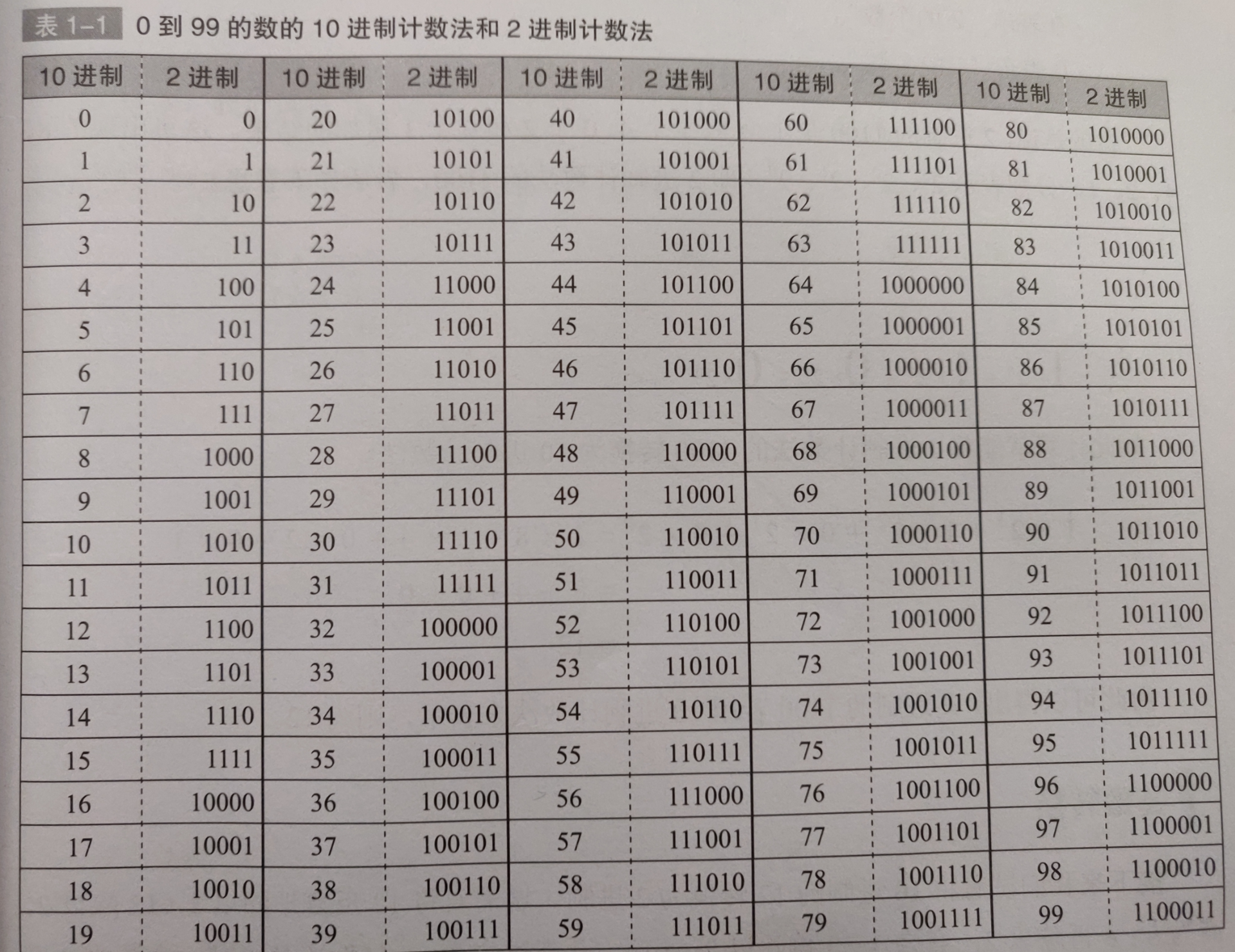
10进制计数法
- 平时我们使用的就是10进制计数法,使用的数字有10种,即
0、1、2、3、4、5、6、7、8、9 - 数位有一定的意义,从右往左分别表示个位、十位、百位、千位...
- 引用书中的例子,来分解
2503这个数- 2 表示的是 1000 的个数
- 5 表示的是 100 的个数
- 0 表示的是 10 的个数
- 3 表示的是 1 的个数
- 2503 这个数字就是2个1000、5个100、0个10、3个1 累加的结果
- 1000 是
10*10*10即10的3次方,100 是10*10即10 的2次方 - 2503 又可以表示为
2*10的3次方 + 5*10的2次方 + 0*10的1次方 + 3*10的0次方
2进制计数法
- 计算机在处理数据时使用的是2进制计数法,使用的数字有2中,即
0、1 - 数位的意义是,从右往左分别表示1位、2位、4位、8位、16位....
10进制和2进制数的转换
2 进制转换成 10 进制
直接举例子,把2进制
1010110转换成10进制
由于2进制从右往左分别表示1位,2位,4位,8位,16位...
| 1 | 0 | 1 | 0 | 1 | 1 | 0 |
|---|---|---|---|---|---|---|
| 64 | 32 | 16 | 8 | 4 | 2 | 1 |
然后把所有的1下面的对应的值加起来,即64+16+4+2=86
10 进制转换成 2 进制
余数短除法
活用这个方法可以将所有十进制数字转换成任何进制表达。除数为2是因为我们最终想得到的以2为基数的数(即二进制数值) 。如果最终想得到其他数系的数字,用目标数系的基数代替这个方法里二进制的基数2 就可以了。例如,要得到基数为9的数,就用9来代替2作为除数 。最终的结果就是目标数系的数字表达。
整个计算过程只需要将数字一直除以2
- 进行除法运算,纪录余数0或1
- 继续用商除以2,一直到商为0
- 写出2进制数字,从最后一个余数开始顺序读,读到最开始的余数
Share
面向切面编程
昨天晚上躺在床上,和我妻子讨论起了AOP,我们举了几个生活中的例子来分析什么是join point、pointcut、以及advice。例如计划一次出游,要去三个地方,到达每个景点后可能要拍照、吃饭或购物。这三个地方就是join point,在某个景点拍吃购的地点为 pointcut,而拍照、吃饭、购物这几件事情是advice,它们在出游进行的过程中被切入pointcut。
附件是我在部门进行的面向切面编程的分享PPT AOP入门